CV

Dynamic Parabolic CBF

PaperTitle
Beyond Collision Cones: Dynamic Obstacle Avoidance for Nonholonomic Robots via Dynamic Parabolic Control Barrier Functions
Author
Hun Kuk Park*, Taekyung Kim*, Dimitra Panagou
Note
(* equal contribution)
Affiliation
Department of Robotics, University of Michigan
Venue
2 more properties
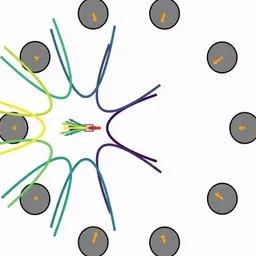
Illustration of the DPCBF mechanism in dynamic obstacle avoidance
We propose a Dynamic Parabolic Control Barrier Function (DPCBF) for nonholonomic robots in dynamic obstacle avoidance tasks. By dynamically shaping its safety boundary based on the distance to and relative velocity of an obstacle, our method provides a less conservative safety margin. Specifically, the parabola’s vertex shifts away from the robot’s origin in proportion to the relative distance, creating a more relaxed safety constraint compared to traditional collision-cone or velocity-obstacle approaches while still guaranteeing safety under input constraints. This less restrictive formulation significantly improves the feasibility of the underlying CBF-based quadratic program (QP), particularly in dense environments where other methods often fail.

Motivation

(left) Illustration of the collision cone CBF (C3BF) mechanism. (right) QP easily becomes infeasible with C3BF.
Methods based on collision cones or velocity obstacles (VO) define the unsafe set as a cone in the relative-velocity space. CBFs based on these methods ensure safety by constraining the robot's relative velocity to remain outside of this cone. However, this strategy has fundamental weaknesses:
•
It's overly conservative: The safety constraint depends only on the angle of the relative velocity, not its magnitude or the actual distance to the obstacle. This means the robot is prohibited from moving toward an obstacle, regardless of its speed or how much collision-free space is available.
•
It fails in dense environments: When a robot is surrounded by many obstacles, the individual collision cones can overlap and eliminate all feasible control options. This causes the underlying QP to become infeasible, leading to mission failure even when a safe path clearly exists

DPCBF

Parabolic safety boundary is defined on the Line-of-Sight (LoS) coordinate frame
Illustration of DPCBF’s safety boundary
Our DPCBF formulation defines a parabolic safety boundary within a Line-of-Sight coordinate frame to explicitly consider both the distance to an obstacle and the relative velocity. DPCBF considers the robot is safe as long as its relative velocity vector stays outside the parabolic region.

Preview Experiments

Scenario 1 (Surrounded by Obstacles)

C3BF
MA-CBF-VO
Dynamic Zone-Based CBF
DPCBF

Scenario 2 (max_obs_radius = 0.3 m)

C3BF
MA-CBF-VO
Dynamic Zone-Based CBF
DPCBF

Scenario 3 (max_obs_radius = 0.5 m)

C3BF
MA-CBF-VO
Dynamic Zone-Based CBF
DPCBF

Scenario 4 (max_obs_radius = 0.7 m)

C3BF
MA-CBF-VO
Dynamic Zone-Based CBF
DPCBF
For more details on the experiments and implementation, please visit our GitHub repository.

Video

BibTex

@inproceedings{park2025dpcbf, author = {Park, Hun Kuk and Kim, Taekyung and Panagou, Dimitra}, title = {Beyond Collision Cones: Dynamic Obstacle Avoidance for Nonholonomic Robots via Dynamic Parabolic Control Barrier Functions}, booktitle = {arXiv preprint arXiv.25}, shorttitle = {DPCBF}, year = {2025} }
LaTeX
복사